The Failings of the Senses and Intuition

Despite the denials of Berkeley, the qualifications of Hume, and the reservations of Heraclitus, Plato, Kant, and Mill concerning what we can know about the external world, physicists and mathematicians do believe that there is an external world. They would argue that even if all human beings were suddenly wiped out, the external or physical world would continue to exist. When a tree crashes to the ground in a forest, a sound is created even if no one is there to hear it. We have five senses--sight, hearing, touch, taste, and smell--and each of these constantly receives messages from this external world. Whether or not our sensations are reliable, we do receive them from some external source.

For practical reasons, such as remaining alive and possibly for improving life in the external world, we certainly want to know as much as possible about this world. We must distinguish land from sea. We must grow food, build shelters, and protect ourselves against wild beasts. Why then can we not rely on our senses to achieve these aims? Primitive civilizations have done so. But just as to the pure in heart the world is pure, so to the simpleminded the world is simple.

In attempting to improve our material way of life, we were forced to extend our knowledge of the external world. Thus we necessarily extended the uses of our senses to the utmost. Unfortunately for us, our senses are not only limited but also deceiving. Trusting solely in the senses can even lead to disaster. Let us note some of these limitations.

 

Of the five senses, the sense of sight is perhaps the most valuable. Let us first test how much we can depend on this sense. We begin with a few simple examples. Through the years, many deceptive visual figure were deliberately conceived and constructed to show the limitations of the eye. In fact, physicists and astronomers of the nineteenth century took a lively interest in visual illusions because they were concerned that visual observations might prove to be unreliable. Wilhelm-Wundt, an assistant to the famous physiologist, physician, and scientist Hermann Von Helmholtz (1821-1894), constructed Figure 1. The illusion is simply that the vertical line looks longer than the horizontal line, which is of equal length. This illusion can be reversed. In Figure 2 the height and width seem equal, but the width is larger.

 The illusion in Figure 3 was devised by Franz Müller-Lyer in 1899
and is also known as the Ernst Mach illusion. The two horizontal lines
are actually the same length.

 

In the Figure 4 the dot is at the middle of the horizontal line, both illusions are created by angles  

  

In Figure 5 the length of the top horizontal line of the lower figure appears shorter than that of the top line of the upper figure. Incidentally, it is difficult to believe that the maximum horizontal width of the lower figure is as great as the maximum height of that figure.

 

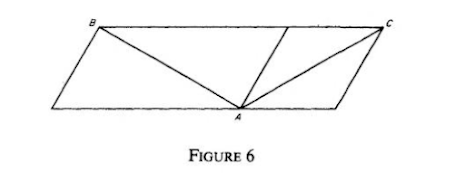
A striking illusion involving the influence of angles is shown in Figure 6. Here the diagonals AB and AC of the two parallelograms are of equal length, but the one on the right appears much shorter

 

If oblique lines are extended across vertical ones, as in Figure 7, the illusion is very striking. The oblique line on the right if extended would meet the upper end of the oblique line on the left; however, the apparent point of intersection is somewhat lower. This well-known illusion is attributed to Johann P. Poggendorf (about 1860).

 

In Figure 8 the three horizontal lines are of equal length, although they appear unequal. This illusion is primarily a result of the sizes of the angles made by the lines at the ends. Within certain limits, the greater the angle the greater is the apparent elongation of the central horizontal portion.

 

A striking illusion of contrast is shown in Figure 9. The central circles of the two figures are equal, although the one surrounded by the large circles appears much smaller than the one surrounded by the smaller circles.

 

Another mechanism is believed to be at work in the Miiller-Lyer illusion. In the left drawing of Figure 10 the horizontal lines at each end of the vertical line A are interpreted as the upper and the lower edges of two walls meeting at a corner. In this case the vertical line would be interpreted as being the foreground of a real-world scene. In the right drawing of Figure 10 the horizontal lines are again seen as wall edges, but in this case they appear to be converging on an inside corner. As a result the vertical line B is interpreted as being in the back¬ ground. The judgment of size constancy then enlarges the perceived length of line B and diminishes line A.

There may be distortions in other types of sensations: temperature, taste, the loudness or pitch of sound, and the speed at which objects appear to move. Let us consider an illusion of temperature. Immerse one hand in a bowl of hot water, the other in a bowl of cold water. After a few minutes, immerse both hands in a bowl of tepid water. Although both hands are now in water of the same temperature, the one that was in hot water feels the tepid as cold while the other feels it as hot. It is interesting to observe that if a hand is placed in water that is then heated (or cooled) gradually so that the change of temperature is not felt, the hand still adapts to the changed temperature.

 

The taste sense is also subject to several illusions. Sweet drinks taste gradually less sweet. Try keeping a strong solution of water and sugar in the mouth for a few seconds and then taste fresh water. It will now taste distinctly salty.

 

Suppose a man drives from New York City to Buffalo (a distance of 400 miles) at 60 miles per hour, and then drives back at 30 miles per hour. What is his average speed? Intuition almost certainly tells us that the average speed is 45 miles per hour. The correct answer, obtained by dividing the total distance by the total time, is about 40 miles per hour.

 

Consider two rectangles with the same perimeter. Must they have the same area? It would seem so. However, a little arithmetic soon tells us that this need not be so. We should then ask, of all rectangles with the same perimeter, which has the largest area? After all, if fencing is to be used to enclose the rectangle and if the area is to be used for planting, then the rectangle with the largest area is most desirable. The answer is a square.

 

A related problem asks us to consider two boxes of the same vol¬ ume. Must the total area of the six sides of each be the same? Let us suppose that each box has a volume of 100 cubic feet. One can have dimensions of 50 by 1 by 2 feet, and the other 5 by 5 by 4 feet. The surface areas in this case are 204 and 130 square feet, respectively. Clearly, the difference is striking

 

 

We all must have this question that- Why are we subject to illusions of the senses and to false intuitions? Examination of the physiology of the various sensory organs could explain the sensory illusions, but for our purposes all we need is to recognize that the human sensory organs and the human brain are involved. With regard to intuition, it is actually a combination of experience, sense impressions, and crude guessing; at best one could say intuition is distilled experience. Subsequent analyses or experiments confirm or discredit it. Intuitions have been characterized as no more than force of habit rooted in psychological inertia.

When we speak of what is certain perceptually, we presuppose a separation between the perception and the perceiver. But this is impossible, because there can be no perception without a perceiver. What, then, is objective? We perhaps naively assume that what all perceivers agree on is objective. There are a sun and a moon. The sun is yellow and the moon is blue.

What is our recourse to countering illusions and erroneous intuitions? The most effective answer is the use of mathematics. Just how effective the subject is remains to be seen. Our chief concern will be to show that there are phenomena in our physical world that are as real as any we perceive through our senses but that are extrasensory or not at all perceptible and, in fact, that in our present culture we utilize and rely on these extrasensory real phenomena, at least as much and perhaps even more than we rely on our sense perceptions.

This is not to say that mathematics does not utilize perceptions and intuitions as suggestions for its own development. However, mathematics surpasses these suggestions much as a diamond surpasses a piece of glass, and what mathematics reveals about our physical world is far more astonishing than the spectacle of the heavens.

Reference book - Mathematics and the search for knowledge.